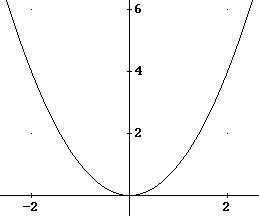
 |
En vanlig presentasjonsmåte er som en graf i et koordinatsystem. |
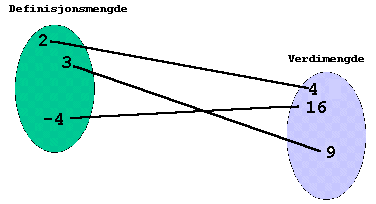 |
Funksjonen kan også representeres ved mengder. Her ser vi definisjonsmengden og verdimengden som områder. Du kan også se verdier i begge mengdene. Strekene mellom verdiene viser hvilke som "hører" sammen. |
| Tallparene kan settes opp i en tabell | |
| f(x) = x+4 | Et algebraisk uttrykk |
La oss se på noen praktiske eksempler:
- Omregning fra antall norske kroner til antall svenske kroner
- Hårfarge i en klasse
- Omregning fra Celsius til Fahrenheit
Har du sett på eksemplene over vil du kanskje ha fått en forståelse for praktiske eksempler på funksjoner. Tenker vi på funksjoner generelt er ofte greit å benytte en modell. Klikk under for å se den såkalte "black box modellen".
Nå kan du prøve noe morsomt
| | Åpningsside | Funksjoner | Grafen | Stigningstall | Sekant | Den deriverte | Oppgaver | ©2007Per G. Østerlie |
