Den deriverte

Hva er den deriverte?

Den deriverte til en funksjon er en ny funksjon som vi skriver:

f'(x)

Denne funksjonen gir oss stigningstallet til tangenten til f(x) i punktet (x,f(x)).

For å forstå denne sammenhengen bedre bør du utforske temaene på denne siden:

1. Tangenten til f(x)
2. Hvordan kan stigningstallet si oss noe om hvordan grafen ser ut
3. Tipp hvilken funksjon du ser den deriverte til

Tangenten til f(x).

På denne sida kan du se nærmere på hva den deriverte er. Prøv å se sammenhengen mellom stigningstallet til tangenten i et punkt og punktet som tegnes opp i koordinatsystemet.

I vinduet under kan du nemlig tegne opp tangenten i et gitt punkt.

For å få tegnet tangenten i et punkt kan du velge to måter. Velg mellom:

• skrive inn x-verdien for tangeringspunktet
• bruke piltastene.

Bruker du piltastene vil tangenten tegnes opp bestemt av verdien til xscl.

Koordinatene til x-verdien og stigningstallet vil vises som et punkt i koordinatsystemet.

For hvert punkt tegnes tangenten opp og stigningstallet merkes av.

Til slutt kan du tegne opp funksjonen som kalles den deriverte.

Bruk god tid til å eksperimentere!

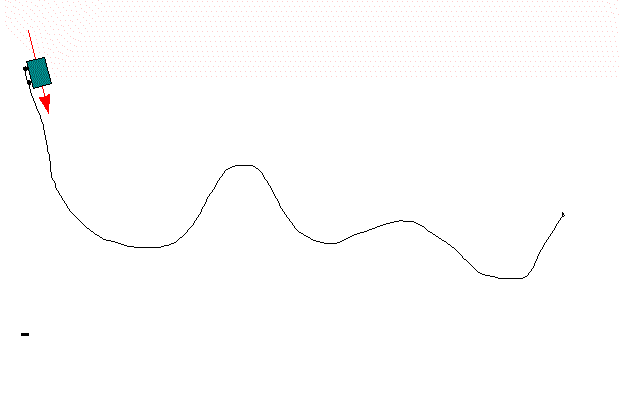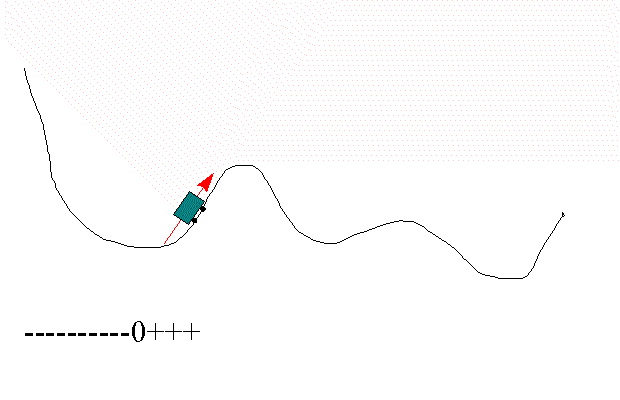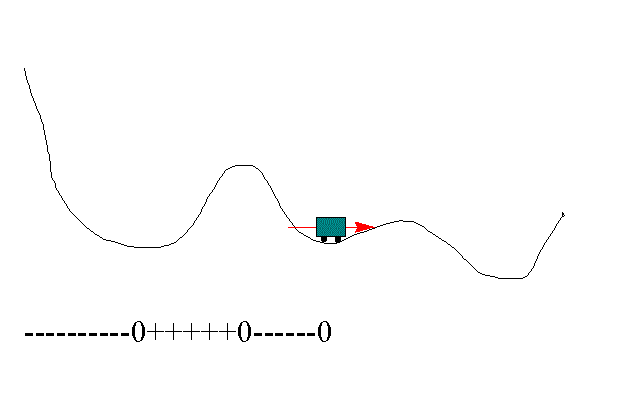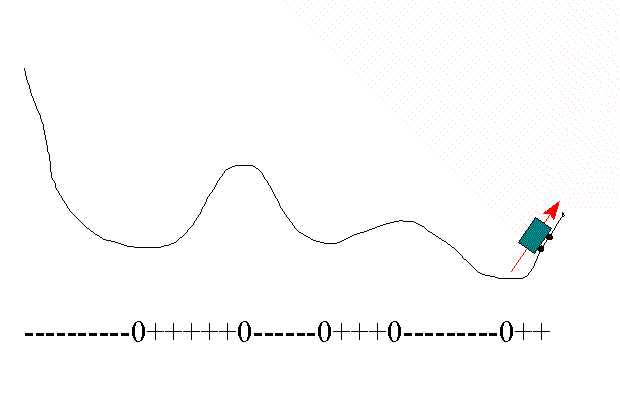
Hvordan kan stigningstallet til tangenten si oss noe om hvordan grafen ser ut?

• Når er stigningstallet null?
• Når er stigningstallet positivt?
• Når er stigningstallet negativt?

Bruk det du vet om stigningstall, se på animasjonen under og prøv å gi svaret.

Kanskje kom du fram til at dette resultatet:

• Der grafen vokser vil stigningstallet til tangenten være positivt
• Der grafen avtar vil stigningstallet til tangenten være negativt
• Der grafen hverken stiger eller synker vil stigningstallet til tangenten være null

Litt omskrevet vil dette resultatet se slik ut:

• f'(x) < 0 når f(x) er avtagende
• f'(x) > 0 når f(x) er voksende
• f'(x) = 0 når f(x) hverken avtar eller vokser. Vi sier at f har et stasjonært punkt.

Dette bruker vi til funksjonsdrøfting!

Tipp hvilken funksjon du ser den deriverte til!

I vinduet under vil du se den deriverte av en funksjon tegnet opp. Din oppgave blir å velge hvilken funksjonen du ser den deriverte til. Tenk på de egenskapene den deriverte funksjonen har mens du får tegnet opp de funksjonene du kan velge mellom. For å se om du har rett: Klikk på en av knappene.

Bruk litt tid for å finne ut hvordan du se hvilken funksjon som er den rette.